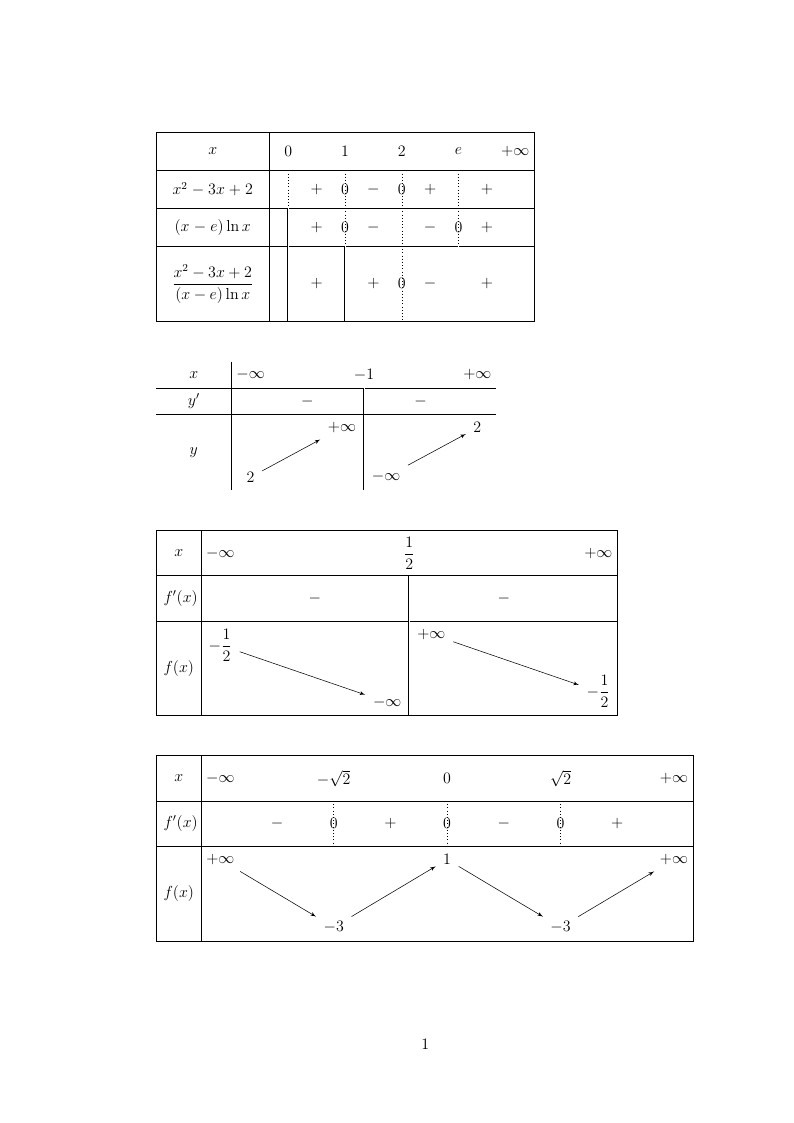
Đây là Bảng biến thiên

\documentclass[12pt,a4paper,oneside]{report}
%======= Packages=======
\usepackage[utf8]{vietnam}
\usepackage{amsmath, amsthm, amssymb}
\usepackage{graphicx}
\usepackage{color}
\usepackage{exscale}
%\usepackage[notref,notcite] {showkeys}
\usepackage[mathscr]{eucal}
\usepackage{enumerate}
\usepackage{fancyhdr}
\usepackage[unicode]{hyperref}
\usepackage[top=35mm, bottom=30mm, left=35mm, right=20mm]{geometry}
\usepackage{tkz-tab}
\begin{document}
\begin{tikzpicture}
\tkzTabInit[lgt=3,espcl=1.5]%
{$x$ /1,
$x^2-3x+2$ /1,
$(x-e)\ln x$ /1,
$\dfrac{x^2-3x+2}{(x-e)\ln x}$ /2}
{$0$ , $1$ , $2$ , $e$ ,$+\infty$}
\tkzTabLine{ t,+,z,-,z,+,t,+,}
\tkzTabLine{ d,+,z,-,t,-,z,+,}
\tkzTabLine{ d,+,d,+,z,-,d,+,}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]
{$x$ /.7, $y'$ /.7,$y$ /2}
{$-\infty$ ,$-1$ , $+\infty$}
\tkzTabLine{ ,-,d,-, }
\tkzTabVar{ - / $2$ ,+D- / $+\infty$/ $-\infty$ , + / $2$ }
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[lgt=1.2,espcl=5]
{$x$ /1.2, $f’(x)$ /1.2,$f(x)$ /2.5}
{$-\infty$ , $\dfrac{1}{2}$ , $+\infty$}
\tkzTabLine{,-,d,-,}
\tkzTabVar{+/$-\dfrac{1}{2}$ ,-D+/$-\infty$/$+\infty$, -/$-\dfrac{1}{2}$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[lgt=1.2,espcl=3]
{$x$ /1.2, $f’(x)$ /1.2,$f(x)$ /2.5}
{$-\infty$ , $-\sqrt{2}$,$0$,$\sqrt{2}$, $+\infty$}
\tkzTabLine{,-,z,+,z,-,z,+,}
\tkzTabVar{+/$+\infty$ ,-/$-3$, +/$1$,-/$-3$,+/$+\infty$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[]
{$u$ /1.2, $f’(u)$ /1.2,$f(u)$ /2.5}
{,$-\dfrac{1}{4}$ , $\dfrac{-1+\sqrt{3}}{2}$ , $+\infty$,}
\tkzTabLine{t,h,d,+,z,-,d,h,t}
\tkzTabVar{LD/,-/$-\dfrac{5}{8}$ ,+/$\dfrac{2-\sqrt{3}}{2}$, -/$-\infty$,}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[lgt=3]%
{$t$/1,%
$f’(t)$ /1,%
$f(t)$ /2}%
{$-\infty$ , $-\frac{2}{3}$ , $\frac{1}{3}$ , $+\infty$}%
\tkzTabLine{ ,-, 0 ,+, 0 ,-, }
\tkzTabVar %
{
+/$0$,-/$-6$ ,+/$3$,-/$0$
}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]
{$x$ /.7, $y'$ /.7,$y$ /2}
{$\frac 12$ ,$\frac 94$ , $4$}
\tkzTabLine{ d,+,0,-,d }
\tkzTabVar{ - / $\sqrt{14}$ ,+/$2\sqrt{7}$ , - / $\sqrt{14}$ }
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]
{$t$/1,$f'(t)$/1,$f(t)$/2}
{$0$,$\frac12$,$+\infty$}
\tkzTabLine{,-,0,+,}
\tkzTabVar{+/$+\infty$,-/ $\frac34$/,+/$+\infty$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$ /1, $f(x)$ /2}
{$-\infty$ , $-\dfrac{2}{3}$ , $\dfrac{1}{3}$ , $+\infty$}
\tkzTabLine{ ,-, 0 ,+, 0 ,-, }
\tkzTabVar {+/$0$,-/$-6$ ,+/$3$,-/$0$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tikzset{h style/.style = {pattern=north west lines}}
\tkzTabInit[nocadre,lgt=2,espcl=3]
{$x$ /1, $f'(x)$ /1,$f(x)$ /2}
{$0$,$3$,$+\infty$}
\tkzTabLine{ d ,+ ,z,-, }
\tkzTabVar{D-/ $-\infty$ , +/ $ \frac{2}{9}$, -/ $0$ / }
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tikzset{h style/.style = {pattern=north west lines}}
\tkzTabInit[nocadre,lgt=2,espcl=3]{$x$ /1, $f'(x)$ /1,$f(x)$ /2}{
$-\infty$,$-2$,$2$,$+\infty$}%
\tkzTabLine{ ,-, d ,h,d ,+, }
\tkzTabVar{+/ $1$ / , -DH/ $-3$ / , D-/ $-5$, +/ $1$ / }
\end{tikzpicture}
\vspace{1cm}
\begin{center}
\textbf{{\Large BANG BIEN THIEN CUA CAC HAM SO THUONG GAP O TRUONG THPT}}
\end{center}
\section{Hàm số bậc hai $\mathbf{y=ax^2+bx+c}$}
\subsection{ Trường hợp $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,-,}
\tkzTabVar{-/ $-\infty$,+/ $y_0$/,-/ $-\infty$}
\end{tikzpicture}
\subsection{ Trường hợp $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,+,}
\tkzTabVar{+/$+\infty$,-/ $y_0$/,+/$+\infty$}
\end{tikzpicture}
\section{Hàm số bậc ba $\mathbf{y=ax^3+bx^2+cx+d}$}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac <0}$ và $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\tkzTabLine{,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\tkzTabLine{,-,}
\tkzTabVar{+/ $+\infty$,-/ $-\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac <0}$ và $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$+\infty$}
\tkzTabLine{,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\tkzTabLine{,+,}
\tkzTabVar{-/ $-\infty$,+/ $+\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac =0}$ và $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,+,}
\tkzTabVar{-/ $-\infty$, R/,+/ $+\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac =0}$ và $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,-,}
\tkzTabVar{+/ $+\infty$, R/,-/ $-\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac >0}$ và $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,+,0,-,0,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,+,0,-,0,+,}
\tkzTabVar{-/ $-\infty$, +/ $y_1$,-/ $y_2$, +/ $+\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac >0}$ và $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,-,0,+,0,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,-,0,+,0,-,}
\tkzTabVar{+/ $+\infty$, -/$y_1$,+/ $y_2$, -/$-\infty$ }
\end{tikzpicture}
\end{document}