MY FAVORITE THEOREM
Author
princess sy
Last Updated
7 年前
License
Creative Commons CC BY 4.0
Abstract
A requirement for our Math330 class.
A requirement for our Math330 class.
\documentclass[12pt]{article}
\usepackage{tikz}
\usepackage{graphicx}
\begin{document}
\title{MY FAVORITE THEOREM}
\author{Princess Sy}
\date{May 12,2016}
\maketitle
\begin{center}
\textbf{PYTHAGOREAN THEOREM}
\end{center}
\begin{center}
\textrm{It states that,the square of \textit{a} plus the square of \textit{b} is equal to the square of \textit{c}.}
\begin{equation}
a^2+b^2=c^2
\end{equation}
\begin{tikzpicture}[scale=1.25]%,cap=round,>=latex]
\coordinate [label=left:$C$] (A) at (-1.5cm,-1.cm);
\coordinate [label=right:$A$] (C) at (1.5cm,-1.0cm);
\coordinate [label=above:$B$] (B) at (1.5cm,1.0cm);
\draw (A) -- node[above] {$a$} (B) -- node[right] {$c$} (C) -- node[below] {$b$} (A);
\draw (1.25cm,-1.0cm) rectangle (1.5cm,-0.75cm);
\end{tikzpicture}
\end{center}
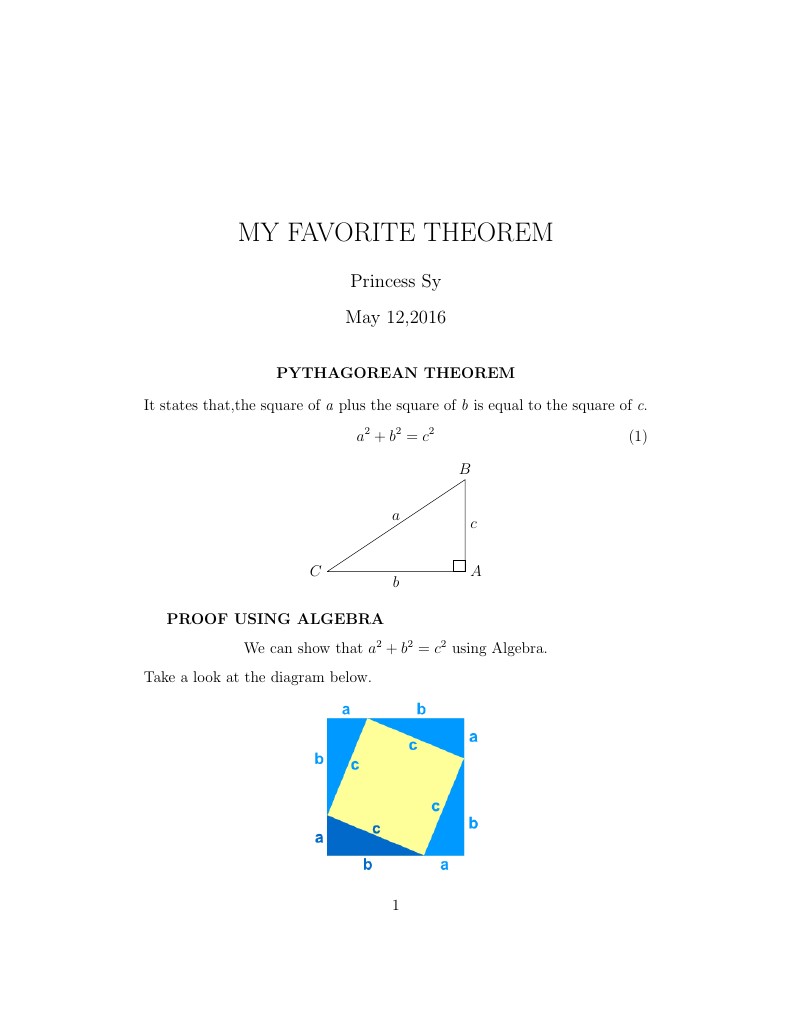
\textbf{PROOF USING ALGEBRA}
\begin{center}
\textrm{We can show that ${a^2+b^2=c^2}$ using Algebra.}
\end{center}
\textrm{Take a look at the diagram below.}
\begin{center}
\includegraphics[scale=.75]{pythagorean-theorem-proof.png}
\end{center}
\section{Area of Whole square}
\textnormal{Each side of the square has a length of $a+b$}
\begin{equation}
A=(a+b)(a+b)
\end{equation}
\section{Area of the Pieces}
\subsection{First, the smaller(tilted) square has an Area}
\begin{equation}
A=c^2
\end{equation}
\subsection{And there are four triangle,each one of them has an Area}
\begin{equation}
A=\frac{1}{2}ab
\end{equation}
\textbf{So all four of them combined}
\begin{equation}
A=4(\frac{1}{2}ab)=2ab
\end{equation}
\subsection{Adding up the Area of the tilted square and the Area of the 4 Triangles}
\begin{equation}
A=c^2 + 2ab
\end{equation}
\section{Conclusion}
\textbf{Let the Area of the Whole Square be Equal to the Area of the Pieces}
\begin{equation}
(a+b)(a+b)=c^2+2ab
\end{equation}
\begin{equation}
a^2+2ab+b^2=c^2+2ab
\end{equation}
\begin{equation}
a^2+2ab+b^2-2ab=c^2+2ab-2ab
\end{equation}
\begin{equation}
a^2+b^2=c^2
\end{equation}
\textup{NOW WE SEE HOW PYTHAGOREAN THEOREM WORKS}
\end{document}